Área de un polígono
Area y perimetro
sábado, 21 de mayo de 2011
¿Como sacar el perimetro?
Polígonos
El perímetro de un polígono se calcula sumando las longitudes de todos sus lados. Así pues, la fórmula para los triángulos es:  , donde
, donde  \,
\,  y
y  son las longitudes de cada lado. Para los cuadriláteros, la ecuación es:
son las longitudes de cada lado. Para los cuadriláteros, la ecuación es:  . Para los polígonos regulares, o equiláteros:
. Para los polígonos regulares, o equiláteros: 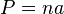 , donde
, donde  es el número de lados y
es el número de lados y  es la longitud del lado.
es la longitud del lado.
 , donde
, donde  \,
\,  y
y  son las longitudes de cada lado. Para los cuadriláteros, la ecuación es:
son las longitudes de cada lado. Para los cuadriláteros, la ecuación es:  . Para los polígonos regulares, o equiláteros:
. Para los polígonos regulares, o equiláteros: 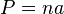 , donde
, donde  es el número de lados y
es el número de lados y  es la longitud del lado.
es la longitud del lado.[editar]Círculos
El perímetro de un círculo es una circunferencia y su longitud es:
ó
donde:
 es la longitud del perímetro
es la longitud del perímetro es la constante matemática pi (π = 3.14159265...)
es la constante matemática pi (π = 3.14159265...) es la longitud del radio
es la longitud del radio es la longitud del diámetro
es la longitud del diámetro
Para obtener el perímetro de un círculo se multiplica el diámetro por pi.
En general
Si se considera la distancia desde el centro de un polígono regular a uno de sus vértices (o en el caso de un círculo, su radio), se cumple lo siguiente
¿Como sacar el área?
Área de figuras planas
Area de un triangulo.
- El área de un triángulo es igual al semiproducto entre la longitud de una base y la altura relativa a esta:3
- donde b es la base del triángulo y h es la altura correspondiente a la base. (se puede considerar cualquier lado como base)
- Si el triángulo es rectángulo, la altura coincide con uno de los catetos, con lo cual el área es igual al semiproducto de los catetos:

- donde a y b son los catetos.
- Si se conoce la longitud de sus lados, se puede aplica la fórmula de Herón.
- donde a, b, c son los valores de las longitudes de sus lados, s = ½ (a + b + c) es el semiperimetro del triángulo.
- Si el triángulo es equilátero, el área es igual a un cuarto del cuadrado de un lado por la raíz cuadrada de 3:
- donde a es un lado del triángulo.
[editar]Área de un cuadrilátero
- El área del trapezoide o de cualquier cuadrilátero es igual al semiproducto de sus diagonales por el seno del angulo que forman.
- El área también se puede obtener mediante triangulación:
- Siendo:
 el ángulo comprendido entre los lados
el ángulo comprendido entre los lados  y
y  .
. el ángulo comprendido entre los lados
el ángulo comprendido entre los lados  y
y  .
.
- El rectángulo es un paralelogramo cuyos ángulos son todos de 90º, y el área es igual al producto de dos de sus lados contiguos a y b:3
- El rombo es un paralelogramo, cuyos 4 lados son iguales, y tiene su área dada por el semiproducto de sus dos diagonales:
- El cuadrado es el polígono regular de cuatro lados; es a la vez un rectángulo y un rombo, por lo que su área puede ser calculada de la misma manera que la de estos dos. En particular, dado que sus lados son iguales, se usa la fórmula:3
- El trapecio, el cual tiene dos lados opuestos paralelos entre sí y dos lados no paralelos, tiene un área que viene dada por la media aritmética de sus lados paralelos multiplicado por la distancia entre ellos (altura):3
[editar]Área del círculo y la elipse
El área de un círculo, o la delimitada por una circunferencia, se calcula mediante la siguiente expresión matemática:4
El área delimitada por una elipse es similar y se obtiene como producto del semieje mayor por el semieje menor multiplicados por π:5
[editar]Área delimitada entre dos funciones
Una forma para hallar el área delimitada entre dos funciones, es utilizando el cálculo integral:
El resultado de esta integral es el área comprendida entre las curvas:  y
y ![g(x) [< f(x)]\,](http://upload.wikimedia.org/math/1/d/3/1d3507ab25c5f1c6f1f965b2397293c3.png) en el intervalo
en el intervalo ![[a,b]\,](http://upload.wikimedia.org/math/7/f/3/7f3408c72246eece3d5542fc853ce417.png) .
.
 y
y ![g(x) [< f(x)]\,](http://upload.wikimedia.org/math/1/d/3/1d3507ab25c5f1c6f1f965b2397293c3.png) en el intervalo
en el intervalo ![[a,b]\,](http://upload.wikimedia.org/math/7/f/3/7f3408c72246eece3d5542fc853ce417.png) .
.- Ejemplo
Si se quiere hallar el área delimitada entre el eje x y la función f(x) = 4 − x2 en el intervalo [ − 2;2], se utiliza la ecuación anterior, en este caso: g(x) = 0entonces evaluando la integral, se obtiene:
Por lo que se concluye que el área delimitada es 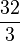 .
.
El volumen encerrado entre dos funciones también puede ser reducido al cálculo de una integral, similar.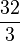 .
.¿Que es el area y el perimetro?
Area:
El área es una medida de la extensión de una superficie, expresada en unidades de medida denominadas superficiales. Para superficies planas el concepto es más intuitivo. Cualquier superficie plana de lados rectos puede triangularse y se puede calcular su área como suma de las áreas de dichos triángulos. Ocasionalmente se usa el término "área" como sinónimo de superficie, cuando no existe confusión entre el concepto geométrico en sí mismo (superficie) y la magnitud métrica asociada al concepto geométrico (área)
Perimetro:
En matemáticas, el perímetro es la medida del contorno de una figura geométrica.
Introduccion
Hola, :)
Este blog fue creado para asesorías matemáticas, con vídeos, explicaciones paginas web, ejercicios todo lo que les pueda ayudar para entender el tema.
Duda o comentario no duden en mandarnos un mensaje o publicar su comentario oki ;) espero que esta pagina sea de su agrado.

Suscribirse a:
Entradas (Atom)



 representa el perímetro,
representa el perímetro, representa el
representa el  representa el
representa el 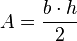
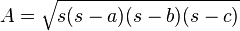
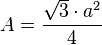










![A(-2,2) = \int^2_{-2} | 4 - x^2 - 0 | dx = 2 \int^2_0 4 - x^2 dx = 2 \left[ 8 - \left(\frac{2^3 - 0}{3}\right) \right] = \frac{32}{3}](http://upload.wikimedia.org/math/0/6/7/06719bebf0dff05ea21b3370585d4927.png)